Plasticity and Grain boundaries¶
The strength of metals and alloys is usually related to the mobility of their dislocations, linear defects of the crystal structure. In polycrystals, crystallographic domains are separated by grain boundaries (GBs) which constitute obstacles to dislocations motion. The famous empirical Hall-Petch 1 law states that the smaller the grains, the harder the material and refining grain size is actually widely employed to harden many structural metals and alloys materials. Ultimately, as in nanocrystals, the grains are so small that no dislocations are present anymore and the material has to find alternative ways to deform. In fact, it often becomes fragile.
Shear-coupled migration¶
Until recently, these alternative mechanisms were difficult to capture experimentally, especially in small-grained materials, and often vaguely designated as "grain-boundary-related plasticity", a term that enclosed processes as different as GB creep, GB sliding, rotation, capillarity and shear-coupling migration. Among those mechanisms that are all poorly known in terms of elementary physical processes, the later has recently focused a lot of attention because of its potential effectiveness: a migrating GB can create a shear perpendicular to its direction of motion, resulting in a plastically release of applied stresses (Fig. 1). The ratio between the shear displacement (d) and the migration distance (m) is called the coupling factor \beta.
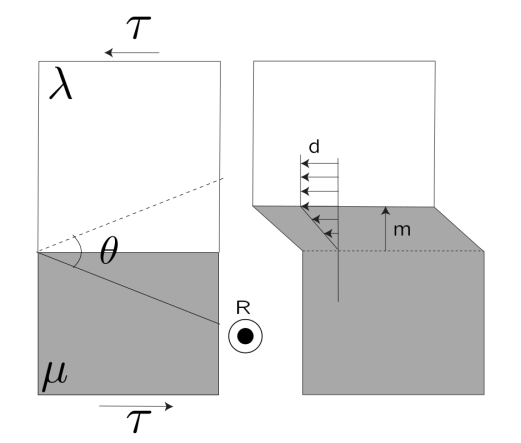
Fig. 1: Shear migration coupling of a symmetric tilt GB of misorientation angle \theta separating the \lambda and \mu grains.
The Cahn-Taylor-Mishin approach¶
The most cited model for this mechanism is the one from Cahn, Mishin & Taylor 2 who adapted and generalized the earlier work from Read and Shockley 3 on low angle GBs. In both models GBs are constituted by a stack of perfect lattice dislocations, which implies that the shear produced during migration scales with the misorientation: the higher the density of dislocations in the GB (according to the Frank-Bilby equation), the higher the misorientation, and also the higher the shear strain when they move.
This hypothesis, verified for low angle GBs, is physically questionable for large angle GBs as the invoked dislocations will overlap each others. In this approach 2 GBs are considered as arrays of perfect lattice dislocations and ignore the fact that real grain boundaries are more complex. Indeed for a given misorientation, topological defects can be treated by the disconnection theory. It is therefore no surprise that the most recent extensive molecular dynamics (MD) simulations (one of the most spread technique to investigate shear-migration coupling in GBs) showed that each migrating GB can adopt not one, but several coupling factors, and thus deliver various amounts of shear for a given GB misorientation 4. So far, most of the atomistic and continuum simulations addressed very specific GBs. Most of the times single, short period, flat GBs, as found in bicrystals 567 8 but also rounded ones 910 or incommensurate GBs 11. Some large MD simulations on specific polycrystals also showed that shear-migration coupling was a highly effective and predominant mechanism over sliding for instance 12.
Experimental works¶
Experimentally, results are much more limited. The group of Aachen in Germany has a long practice of macroscopic Al bi-crystals processing and deformation where they can measure the coupling factor at a macro-scale 131415. Similar experiments were scarcely carried out in Japan 16. In small-grained materials, TEM or X-ray-based experiments showed that stress-assisted grain growth really occurs, but the detailed mechanisms resist investigations 171819. High Resolution TEM (HRTEM) is also very helpful as it can reveal the atomic structure of many static GBs are 2021 but technical restrictions such as perfect zone-axis orientation or poor control of the applied stress limit its outcome regarding migrating GBs. Many groups are now using specific techniques able to map the crystallographic orientations of polycrystals under stress 222324 to obtain a statistical view of the behaviors of an ensemble of grains and then pinpoint the behavior of GBs and grains depending on their orientation (Fig. 2) 2526. As a matter of fact, the topological knowledge of one GB behavior requires the knowledge of its structure (and its chemistry) at a microscopic and atomic scale 2127. GB properties do not depend only on the three macroscopic parameters of the misorientation, but equally importantly on other parameters such as the GB plane (two macroscopic parameters for the orientation and one microscopic one for the position), and the translation between both crystals (3 microscopic parameters). What the most recent studies point out is that one cannot attribute a behavior to a type of GB depending knowing its misorientation and habit plane on 26. Extrinsic defects and disconnections content may play a more pivotal role 20282930.

Fig. 2. Evolution of the microstructure of a 500 nm thick gold film during cyclic loading. The grain orientation maps in the strain direction (SD) are obtained in EBSD before (left), and after 1000 cycles at 1.5% peak strain (right). Selected grains coarsen during the deformation (numbers 1 to 10). The low-angle, high-angle and twin grain boundaries are coded by different colors as stated (after 23). No specific grain orientation nor GB misorientation seems prominent in grain growth.
Our previous contributions¶
In 2008, we started looking at the problem by using in situ TEM 31. They were the first to experimentally quantify the coupling factor in small-grained polycrystals and to show that the measurements did not match the Cahn-Mishin-Taylor model. In a following PhD thesis combining HRTEM, in situ straining of small-grained and bi-crystalline aluminum (provided by the Aachen group) and Molecular Dynamics was able to show that some of the shear-coupled migration of GBs was the result of disconnections motion inside these GBs 2832. Focusing on the energy transition in MD models using the Nudge Elastic Band method, we further demonstrated that disconnection motion was the elemental mechanism at the source of GB coupled motion under stress 33 (Fig. 3).
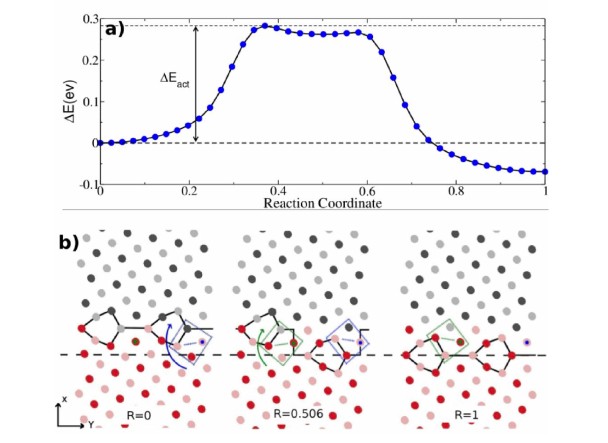
Fig. 3. MD simulations of the nucleation and propagation of a disconnection in a virtual bicrystal containing a \Sigma 13 grain boundary. The minimum energy path (upper) correspond to the nucleation and propagation of a disconnection (described below) that leads to the GB migration.
Recently, we have extended the in situ TEM methodology with automatic crystalline orientation mapping (ACOM) to study grain rotation (Fig. 4) 34 and GB sliding using Micro ElectroMechanical Systems (MEMS) in situ platforms 35, and showed that both these mechanisms are also disconnections-based. Because disconnections are GB-bound defects, they possess both a dislocation and a step component 36. They are also called "step-dislocations". The dislocation component can couple with the stress and move while the step propagation generates the migration. The ratio between the Burgers vector length and the step height is the coupling factor.

Fig. 4. Evolution of the microstructure of a 250 nm thick Al film during tensile loading. The orientation maps are obtained with the ACOM system in a TEM. The figures below were extracted from an in situ sequence where disconnections (d, arrows) are seen to travel along the G1/G27 grain boundary. The identified disconnections d are associated with a rotation between both grains G1 and G27 (after [35]).
The big picture emerging from these recent studies is that disconnections are a key element in understanding all GB-based mechanisms.
-
E.O. Hall, The Deformation and Ageing of Mild Steel: III Discussion of Results, Proceedings of the Physical Society Section B. 64 (1951) 747–753, and N.J. Petch, The cleavage strength of polycrystals, Journal of the Iron Steel Institute. 174 (1953) 25–28. ↩
-
J.W. Cahn, Y. Mishin, A. Suzuki, Coupling grain boundary motion to shear deformation, Acta Materialia. 54 (2006) 4953–4975. ↩↩
-
W.T. Read, W. Shockley, Imperfections in Nearly Perfect Crystals, 1957. ↩
-
D.L. Olmsted, E.A. Holm, S.M. Foiles, Survey of computed grain boundary properties in face-centered cubic metals--II: Grain boundary mobility, Acta Materialia. 57 (2009) 3704–3713. ↩
-
K. Cheng, L. Zhang, C. Lu, K. Tieu, Coupled grain boundary motion in aluminium: the effect of structural multiplicity, Scientific Reports. 6 (2016) 25427. ↩
-
Y. Guo, J. Wang, Z. Wang, J. Li, Y. Yang, Y. Zhou, Effects of a disconnection dipole on the shear- coupled grain boundary migration, Computational Materials Science. 109 (2015) 253–257. ↩
-
L. Wan, W. Han, K. Chen, Bi-crystallographic lattice structure directs grain boundary motion under shear stress, Scientific Reports. 5 (2015) 13441. ↩
-
E.R. Homer, S. Patala, J.L. Priedeman, Grain Boundary Plane Orientation Fundamental Zones and Structure-Property Relationships, Scientific Reports. 5 (2015). ↩
-
L.A. Barrales-Mora, J.-E. Brandenburg, D.A. Molodov, Impact of grain boundary character on grain rotation, Acta Materialia. 80 (2014) 141–148. ↩
-
D.A. Molodov, L.A. Barrales-Mora, J.-E. Brandenburg, Grain boundary motion and grain rotation in aluminum bicrystals: recent experiments and simulations, IOP Conf. Ser.: Mater. Sci. Eng. 89 (2015) 012008. ↩
-
M.L. Bowers, C. Ophus, A. Gautam, F. Lançon, U. Dahmen, Step Coalescence by Collective Motion at an Incommensurate Grain Boundary, Phys. Rev. Lett. 116 (2016) 106102. ↩
-
J. Schäfer, K. Albe, Competing deformation mechanisms in nanocrystalline metals and alloys: Coupled motion versus grain boundary sliding, Acta Materialia. 60 (2012) 6076–6085. ↩
-
D.A. Molodov, T. Gorkaya, G. Gottstein, Dynamics of grain boundaries under applied mechanical stress, J Mater Sci. 46 (2011) 4318–4326. ↩
-
D.A. Molodov, V.A. Ivanov, G. Gottstein, Low angle tilt boundary migration coupled to shear deformation, Acta Materialia. 55 (2007) 1843. ↩
-
T. Gorkaya, D.A. Molodov, G. Gottstein, Stress-driven migration of symmetrical \langle 100 \rangle tilt grain boundaries in Al bicrystals, Acta Materialia. 57 (2009) 5396–5405. ↩
-
H. Fukutomi, T. Kamijo, Grain boundary sliding-migration of aluminum \langle 100 \rangle \Sigma 11 {113} symmetric tilt coincidence grain boundary and its interpretation based on the motion of perfect DSC dislocations, Scripta Metallurgica. 19 (1985) 195–197. ↩
-
T.J. Rupert, D.S. Gianola, Y. Gan, K.J. Hemker, Experimental observation of stress-driven grain boundary migration, Science. 326 (2009) 1686–1690. ↩
-
M. Legros, S.D. Gianola, K.J. Hemker, In situ TEM observations of fast grain-boundary motion in stressed nanocrystalline aluminum films, Acta Materialia. 56 (2008) 3380–3393. ↩
-
S. Schmidt, S.F. Nielsen, C. Gundlach, L. Margulies, X. Huang, D.J. Jensen, Watching the Growth of Bulk Grains During Recrystallization of Deformed Metals, Science. 305 (2004) 229–232. ↩
-
M. Sennour, S. Lartigue-Korinek, Y. Champion, M.J. Hÿtch, HRTEM study of defects in twin boundaries of ultra-fine grained copper, Philosophical Magazine. 87 (2007) 1465–1486. ↩↩
-
O.H. Duparc, J.P. Couzinie, J. Thibault-Pénisson, Atomic structures of symmetrical and asymmetrical facets in a near \Sigma 9 {221} tilt grain boundary in copper, Acta Materialia. (2007). ↩↩
-
E.F. Rauch, M. Veron, J. Portillo, D. Bultreys, Y. Maniette, S. Nicolopoulos, Automatic crystal orientation and phase mapping in TEM by precession diffraction, Microsc. and Anal. 93 (2008) S5–S8. ↩
-
A.K. Kiss, E.F. Rauch, J.L. Lábár, Highlighting material structure with transmission electron diffraction correlation coefficient maps, Ultramicroscopy. 163 (2016) 31–37. ↩↩
-
A. Kobler, A. Kashiwar, H. Hahn, C. Kübel, Combination of in situ straining and ACOM TEM: A novel method for analysis of plastic deformation of nanocrystalline metals, Ultramicroscopy. 128 (2013) 68–81. ↩
-
P.W. Trimby, Y. Cao, Z. Chen, S. Han, K.J. Hemker, J. Lian, et al., Characterizing deformed ultrafine-grained and nanocrystalline materials using transmission Kikuchi diffraction in a scanning electron microscope, Acta Materialia. 62 (2014) 69–80. ↩
-
O. Glushko, M.J. Cordill, The driving force governing room temperature grain coarsening in thin gold films, Scripta Materialia. 130 (2017) 42–45. ↩↩
-
J.-P. Couzinié, O.H. Duparc, S. Lartigue-Korinek, J. Thibault-Pénisson, B. Décamps, L. Priester, On the atomic structure of an asymmetrical near \Sigma = 27 grain boundary in copper, Philos. Mag. Lett. 89 (2009) 757–767. ↩
-
A. Rajabzadeh, F. Mompiou, S. Lartigue-Korinek, The role of disconnections in deformation-coupled grain boundary migration, Acta Materialia. 77 (2014) 223–235. ↩↩
-
S. Lartigue-Korinek, O.H. Duparc, K.P.D. Lagerlöf, S. Moulahem, A. Hallil, Analysis of dissociated dislocations in a deformed bicrystal close to the rhombohedral twin orientation in α-alumina, Philosophical Magazine. 93 (2013) 1182–1196. ↩
-
S. Poulat, B. Decamps, L. Priester, Weak-beam transmission electron microscopy study of dislocation accommodation processes in nickel \Sigma= 3 grain boundaries, Philosophical Magazine A. (1998). ↩
-
F. Mompiou, D. Caillard, M. Legros, Grain boundary shear--migration coupling—I. In situ TEM straining experiments in Al polycrystals, Acta Materialia. 57 (2009) 2198–2209. ↩
-
A. Rajabzadeh, M. Legros, N. Combe, F. Mompiou, D.A. Molodov, Evidence of grain boundary dislocation step motion associated to shear-coupled grain boundary migration, Philosophical Magazine. ↩
-
A. Rajabzadeh, F. Mompiou, M. Legros, N. Combe, Elementary Mechanisms of Shear-Coupled Grain Boundary Migration, Phys. Rev. Lett. 110 (2013) 265507. ↩
-
F. Mompiou, M. Legros, Quantitative grain growth and rotation probed by in-situ TEM straining and orientation mapping in small grained Al thin films, Scipta Materialia, 99 (2015) 5–8. ↩
-
E. Hosseinian, M. Legros, O.N. Pierron, Quantifying and observing viscoplasticity at the nanoscale: highly localized deformation mechanisms in ultrathin nanocrystalline gold films, Nanoscale. 8 (2016). ↩
-
H.A. Khater, A. Serra, R.C. Pond, J.P. Hirth, The disconnection mechanism of coupled migration and shear at grain boundaries, Acta Materialia. 60 (2012) 2007–2020. ↩